Making Predictions Using Redox Potentials (Electrode Potentials)
This page explains how to use redox potentials (electrode potentials) to predict the feasibility of redox reactions. It also looks at how you go about choosing a suitable oxidising agent or reducing agent for a particular reaction.
Important: This is the final page in a sequence of five pages about redox potentials. You will find it much easier to understand if you start from the beginning. Links at the bottom of each page will bring you back here again.
Don't try to short-cut this. Redox potentials are absolutely simple to work with if you understand what they are about. If you don't, the whole topic can be a complete nightmare!
Predicting the Feasibility of a Possible Redox Reaction
A Reminder of What You Need to Know
Standard electrode potentials (redox potentials) are one way of measuring how easily a substance loses electrons. In particular, they give a measure of relative positions of equilibrium in reactions such as:
\begin{matrix}
\text{Zn}^{2+}_{(aq)} + 2\text{e}^- \xrightleftharpoons{} \text{Zn}_{(s)} & E^o = {-}0.76 \text{ V} \\
\\
\text{Cu}^{2+}_{(aq)} + 2\text{e}^- \xrightleftharpoons{} \text{Cu}_{(s)} & E^o = {+}0.34 \text{ V}
\end{matrix}
The more negative the E° value, the further the position of equilibrium lies to the left. Remember that this is always relative to the hydrogen equilibrium – and not in absolute terms.
The negative sign of the zinc E° value shows that it releases electrons more readily than hydrogen does. The positive sign of the copper E° value shows that it releases electrons less readily than hydrogen.
Whenever you link two of these equilibria together (either via a bit of wire, or by allowing one of the substances to give electrons directly to another one in a test tube) electrons flow from one equilibrium to the other. That upsets the equilibria, and Le Chatelier's Principle applies. The positions of equilibrium move – and keep on moving if the electrons continue to be transferred.
The two equilibria essentially turn into two one-way reactions:
- The equilibrium with the more negative (or less positive) E° value will move to the left.
- The equilibrium with the more positive (or less negative) E° value will move to the right.
Note: If you aren't confident about this, please go back and start from the beginning of this sequence of pages. All these ideas are explored in a gentle and logical way. Links at the bottom of each page will bring you back here again.
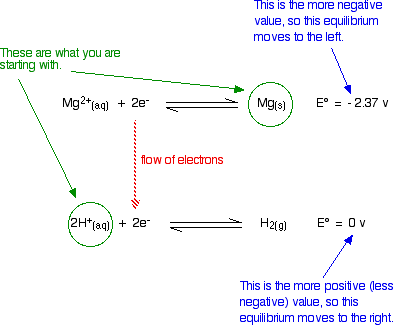
Will Magnesium React With Dilute Sulfuric acid?
Of course it does! I'm choosing this as an introductory example because everybody will know the right answer before we start. We have also explored this from a slightly different point of view on the previous page in this sequence.
The E° values are:
\begin{matrix}
\text{Mg}^{2+}_{(aq)} + 2\text{e}^- \xrightleftharpoons{} \text{Mg}_{(s)} & E^o = {-}2.37 \text{ V} \\
\\
2\text{H}^+_{(aq)} + 2\text{e}^- \xrightleftharpoons{} \text{H}_{2(g)} & E^o = 0 \text{ V} \\
\end{matrix}
You are starting with magnesium metal and hydrogen ions in the acid. The sulfate ions are spectator ions and play no part in the reaction.
Think of it like this. There is no need to write anything down unless you want to. With a small amount of practice, all you need to do is just look at the numbers.
Is there anything to stop the sort of movements we have suggested? No! The magnesium can freely turn into magnesium ions and give electrons to the hydrogen ions producing hydrogen gas. The reaction is feasible.
Now for a reaction which turns out not to be feasible
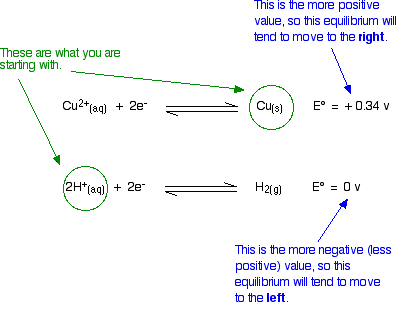
Will Copper React With Dilute Sulfuric acid?
You know that the answer is that it won't. How do the E° values predict this?
\begin{matrix}
\text{Cu}^{2+}_{(aq)} + 2\text{e}^- \xrightleftharpoons{} \text{Cu}_{(s)} & E^o = {+}0.34 \text{ V} \\
\\
2\text{H}^+_{(aq)} + 2\text{e}^- \xrightleftharpoons{} \text{H}_{2(g)} & E^o = 0 \text{ V} \\
\end{matrix}
Doing the same sort of thinking as before:
The diagram shows the way that the E° values are telling us that the equilibria will tend to move. Is this possible? No!
If we start from copper metal, the copper equilibrium is already completely to the right. If it were to react at all, the equilibrium will have to move to the left – directly opposite to what the E° values are saying.
Similarly, if we start from hydrogen ions (from the dilute acid), the hydrogen equilibrium is already as far to the left as possible. For it to react, it would have to move to the right – against what the E° values demand.
There is no possibility of a reaction.
In the next couple of examples, decide for yourself whether or not the reaction is feasible before you read the text.
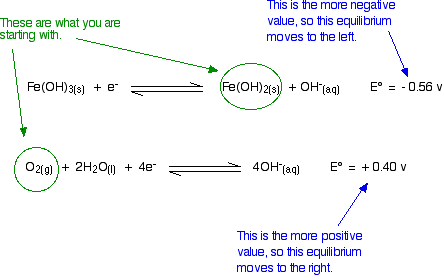
Will Oxygen Oxidise Iron(II) hydroxide to Iron(III) hydroxide Under Alkaline Conditions?
\begin{matrix}
\text{Fe}(\text{OH})_{3(s)} + \text{e}^- \xrightleftharpoons{} \text{Fe}(\text{OH})_{2(s)} + {}^-\text{OH}_{(aq)} & E^o = {-}0.56 \text{ V} \\
\\
\text{O}_{2(g)} + 2\text{H}_2\text{O}_{(l)} + 4\text{e}^- \xrightleftharpoons{} 4\text{OH}^-_{(aq)} & E^o = {+}0.40 \text{ V} \\
\end{matrix}
Think about this before you read on. Remember that the equilibrium with the more negative E° value will tend to move to the left. The other one tends to move to the right. Is that possible?
Yes, it is possible. Given what we are starting with, both of these equilibria can move in the directions required by the E° values. The reaction is feasible.
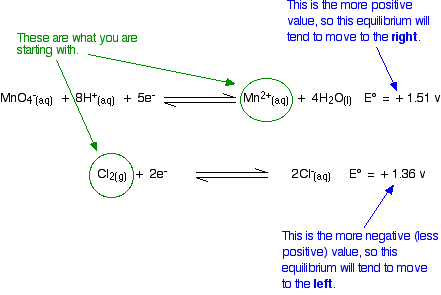
Will Chlorine Oxidise Manganese(II) ions to Manganate(VII) ions?
\begin{matrix}
{\text{MnO}_4}^-_{(aq)} + 8\text{H}^+_{(aq)} + 5\text{e}^- \xrightleftharpoons{} \text{Mn}^{2+}_{(aq)} + 4\text{H}_2\text{O}_{(l)} & E^o = {+}1.51 \text{ V} \\
\\
\text{Cl}_{2(g)} + 2\text{e}^- \xrightleftharpoons{} 2\text{Cl}^-_{(aq)} & E^o = {+}1.36 \text{ V} \\
\end{matrix}
Again, think about this before you read on.
Given what you are starting from, these equilibrium shifts are impossible. The manganese equilibrium has the more positive E° value and so will tend to move to the right. However, because we are starting from manganese(II) ions, it is already as far to the right as possible. In order to get any reaction, the equilibrium would have to move to the left. That is against what the E° values are saying.
This reaction isn't feasible.
Will Dilute Nitric acid React With Copper?
This is going to be more complicated because there are two different ways in which dilute nitric acid might possibly react with copper. The copper might react with the hydrogen ions or with the nitrate ions. Nitric acid reactions are always more complex than the simpler acids like sulfuric or hydrochloric acid because of this problem.
Here are the E° values:
\begin{matrix}
\text{Cu}^{2+}_{(aq)} + 2\text{e}^- \xrightleftharpoons{} \text{Cu}_{(s)} & E^o = {+}0.34 \text{ V} \\
\\
2\text{H}^+_{(aq)} + 2\text{e}^- \xrightleftharpoons{} \text{H}_{2(g)} & E^o = 0 \text{ V} \\
\\
{\text{NO}_3}^-_{(aq)} + 4\text{H}^+_{(aq)} + 3\text{e}^- \xrightleftharpoons{} \text{NO}_{(g)} + 2\text{H}_2\text{O}_{(l)} & E^o = {+}0.96 \text{ V}
\end{matrix}
We have already discussed the possibility of copper reacting with hydrogen ions further up this page. Go back and look at it again if you need to, but the argument (briefly) goes like this:
The copper equilibrium has a more positive E° value than the hydrogen one. That means that the copper equilibium will tend to move to the right and the hydrogen one to the left.
However, if we start from copper and hydrogen ions, the equilibria are already as far that way as possible. Any reaction would need them to move in the opposite direction to what the E° values want. The reaction isn't feasible.
What about a reaction between the copper and the nitrate ions?
This is feasible. The nitrate ion equilibrium has the more positive E° value and will move to the right. The copper E° value is less positive. That equilibrium will move to the left. The movements that the E° values suggest are possible, and so a reaction is feasible.
Copper(II) ions are produced together with nitrogen monoxide gas.
Warning! There are all sorts of ways of dealing with this feasibility question – all of them, I believe, more complicated than this. Some methods actually force you to do some (simple) calculations. Unfortunately, some examiners ask questions which make you use their own inefficient methods of working out whether a reaction is feasible, and you need to know if this is going to be a problem.
UK A-level students should refer to their syllabuses and past papers. Follow this link if you haven't got the necessary information.
You will find the calculation approach covered in my chemistry calculations book, together with more examples using the method developed on these pages. However, I find the calculation approach so pointless that I refuse to include it on this site! Why do a calculation if you can just look at two numbers and decide in seconds whether or not a reaction is feasible?
Two Examples Where the E° Values Seem to Give the Wrong Answer
It sometimes happens that E° values suggest that a reaction ought to happen, but it doesn't. Occasionally, a reaction happens although the E° values seem to be the wrong way around. These next two examples explain how that can happen. By coincidence, both involve the dichromate(VI) ion in potassium dichromate(VI).
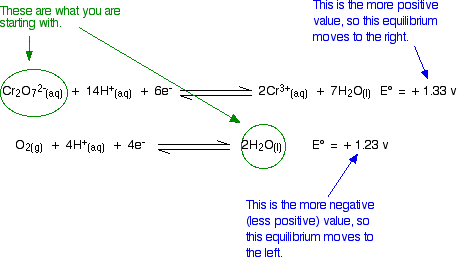
Will acidified potassium dichromate(VI) oxidise water?
The E° values are:
\begin{matrix}
{\text{Cr}_2\text{O}_7}^{2-}_{(aq)} + 14\text{H}^+_{(aq)} + 6\text{e}^- \xrightleftharpoons{} 2\text{Cr}^{3+}_{(aq)} + 7\text{H}_2\text{O}_{(l)} & E^o = {+}1.33 \text{ V} \\
\\
\text{O}_{2(g)} + 4\text{H}^+_{(aq)} + 4\text{e}^- \xrightleftharpoons{} 2\text{H}_2\text{O}_{(l)} & E^o = {+}1.23 \text{ V}
\end{matrix}
The relative sizes of the E° values show that the reaction is feasible:
However, in the test tube nothing happens however long you wait. An acidified solution of potassium dichromate(VI) doesn't react with the water that it is dissolved in. So what is wrong with the argument?
In fact, there is nothing wrong with the argument. The problem is that all the E° values show is that a reaction is possible. They don't tell you that it will actually happen. There may be very large activation barriers to the reaction which prevent it from taking place.
Always treat what E° values tell you with some caution. All they tell you is whether a reaction is feasible – they tell you nothing about how fast the reaction will happen.
Will acidified potassium dichromate(VI) oxidise chloride ions to chlorine?
The E° values are:
\begin{matrix}
{\text{Cr}_2\text{O}_7}^{2-}_{(aq)} + 14\text{H}^+_{(aq)} + 6\text{e}^- \xrightleftharpoons{} 2\text{Cr}^{3+}_{(aq)} + 7\text{H}_2\text{O}_{(l)} & E^o = {+}1.33 \text{ V} \\
\\
\text{Cl}_{2(g)} + 2\text{e}^- \xrightleftharpoons{} 2\text{Cl}^-_{(aq)} & E^o = {+}1.36 \text{ V}
\end{matrix}
Because the chlorine E° value is slightly greater than the dichromate(VI) one, there shouldn't be any reaction. For a reaction to occur, the equilibria would have to move in the wrong directions.
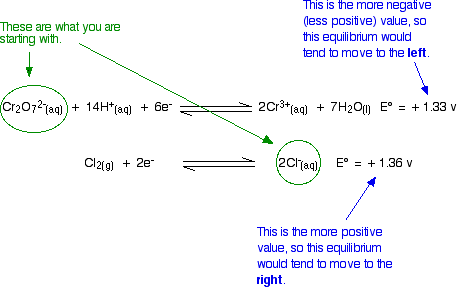
Unfortunately, in the test tube, potassium dichromate(VI) solution does oxidise concentrated hydrochloric acid to chlorine. The hydrochloric acid serves as the source of the hydrogen ions in the dichromate(VI) equilibrium and of the chloride ions.
The problem here is that E° values only apply under standard conditions. If you change the conditions you will change the position of an equilibrium – and that will change its E value. (Notice that you can't call it an E° value any more, because the conditions are no longer standard.)
The standard condition for concentration is 1 mol dm-3. But concentrated hydrochloric acid is approximately 10 mol dm-3. The concentrations of the hydrogen ions and chloride ions are far in excess of standard.
What effect does that have on the two positions of equilibrium?
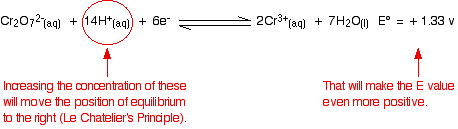
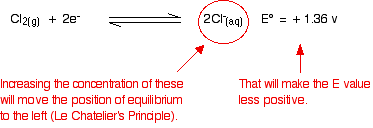
Because the E° values are so similar, you don't have to change them very much to make the dichromate(VI) one the more positive. As soon as that happens, it will react with the chloride ions to produce chlorine.
In most cases, there is enough difference between E° values that you can ignore the fact that you aren't doing a reaction under strictly standard conditions. But sometimes it does make a difference. Be careful!
Selecting an Oxidising or Reducing Agent for a Reaction
There is nothing remotely new in this. It is just a slight variation on what we've just been looking at.
Choosing an Oxidising Agent
Remember: OIL RIG
Oxidation is Loss of electrons; Reduction is Gaining of electrons
- An oxidising agent oxidises something by removing electrons from it. That means that the oxidising agent gains electrons.
It is easier to explain this with a specific example. What could you use to oxidise iron(II) ions to iron(III) ions? The E° value for this reaction is:
\begin{matrix}
\text{Fe}^{3+}_{(aq)} + \text{e}^- \xrightleftharpoons{} \text{Fe}^{2+}_{(aq)} & E^o = {+}0.77 \text{ V}
\end{matrix}
To change iron(II) ions into iron(III) ions, you need to persuade this equilibrium to move to the left. That means that when you couple it to a second equilibrium, this iron E° value must be the more negative (less positive one).
You could use anything which has a more positive E° value. For example, you could use any of the these which we have already looked at over the last page or two:
Dilute nitric acid:
\begin{matrix}
{\text{NO}_3}^-_{(aq)} + 4\text{H}^+_{(aq)} + 3\text{e}^- \xrightleftharpoons{} \text{NO}_{(g)} + 2\text{H}_2\text{O}_{(l)} & E^o = {+}0.96 \text{ V}
\end{matrix}
Acidified potassium dichromate(VI):
\begin{matrix}
{\text{Cr}_2\text{O}_7}^{2-}_{(aq)} + 14\text{H}^+_{(aq)} + 6\text{e}^- \xrightleftharpoons{} 2\text{Cr}^{3+}_{(aq)} + 7\text{H}_2\text{O}_{(l)} & E^o = {+}1.33 \text{ V}
\end{matrix}
Chlorine:
\begin{matrix}
\text{Cl}_{2(g)} + 2\text{e}^- \xrightleftharpoons{} 2\text{Cl}^-_{(aq)} & E^o = {+}1.36 \text{ V}
\end{matrix}
Acidified potassium manganate(VII):
\begin{matrix}
{\text{MnO}_4}^-_{(aq)} + 8\text{H}^+_{(aq)} + 5\text{e}^- \xrightleftharpoons{} \text{Mn}^{2+}_{(aq)} + 4\text{H}_2\text{O}_{(l)} & E^o = {+}1.51 \text{ V}
\end{matrix}
Choosing a Reducing Agent
Remember: OIL RIG
Oxidation is Loss of electrons; Reduction is Gaining of electrons
- A reducing agent reduces something by giving electrons to it. That means that the reducing agent loses electrons.
You have to be a little bit more careful this time, because the substance losing electrons is found on the right-hand side of one of these redox equilibria. Again, a specific example makes it clearer.
For example, what could you use to reduce chromium(III) ions to chromium(II) ions? The E° value is:
\begin{matrix}
\text{Cr}^{3+}_{(aq)} + \text{e}^- \xrightleftharpoons{} \text{Cr}^{2+}_{(aq)} & E^o = {-}0.41 \text{ V}
\end{matrix}
You need this equilibrium to move to the right. That means that when you couple it with a second equilibrium, this chromium E° value must be the most positive (least negative).
In principle, you could choose anything with a more negative E° value – for example, zinc:
\begin{matrix}
\text{Zn}^{2+}_{(aq)} + 2e^- \xrightleftharpoons{} \text{Zn}_{(s)} & E^o = {-}0.76 \text{ V}
\end{matrix}
You would have to remember to start from metallic zinc, and not zinc ions. You need this second equilibrium to be able to move to the left to provide the electrons. If you started with zinc ions, it would already be on the left – and would have no electrons to give away. Nothing could possibly happen if you mixed chromium(III) ions and zinc ions.
That is fairly obvious in this simple case. If you were dealing with a more complicated equilibrium, you would have to be careful to think it through properly.