Orders of Reaction and Mechanisms

This page looks at the relationship between orders of reaction and mechanisms in some simple cases. It explores what a mechanism is, and the idea of a rate determining step. It also explains the difference between the sometimes confusing terms "order of reaction" and "molecularity of reaction".

In any chemical change, some bonds are broken and new ones are made. Quite often, these changes are too complicated to happen in one simple stage. Instead, the reaction may involve a series of small changes one after the other.

A reaction mechanism describes the one or more steps involved in the reaction in a way which makes it clear exactly how the various bonds are broken and made. The following example comes from organic chemistry. It doesn't matter in the least if it is unfamiliar to you!

This is a reaction between 2-bromo-2-methylpropane and the hydroxide ions from sodium hydroxide solution:

The overall reaction replaces the bromine atom in the organic compound by an OH group.

The first thing that happens is that the carbon-bromine bond in a small proportion of the organic compound breaks to give ions:

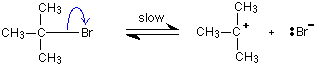
Carbon-bromine bonds are reasonably strong, so this is a slow change. If the ions hit each other again, the covalent bond will reform. The curly arrow in the equation shows the movement of a pair of electrons.

If there is a high concentration of hydroxide ions present, the positive ion stands a high chance of hitting one of those. This step of the overall reaction will be very fast. A new covalent bond is made between the carbon and the oxygen, using one of the lone pairs on the oxygen atom.

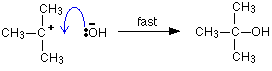
Because carbon-oxygen bonds are strong, once the OH group has attached to the carbon atom, it tends to stay attached.

The mechanism shows that the reaction takes place in two steps and describes exactly how those steps happen in terms of bonds being broken or made. It also shows that the steps have different rates of reaction – one slow and one fast.

The overall rate of a reaction (the one which you would measure if you did some experiments) is controlled by the rate of the slowest step. In the example above, the hydroxide ion can't combine with the positive ion until that positive ion has been formed. The second step is in a sense waiting around for the first slow step to happen.

The slow step of a reaction is known as the rate-determining step.

As long as there is a lot of difference between the rates of the various steps, when you measure the rate of a reaction, you are actually measuring the rate of the rate determining step.

The examples we use at this level are the very simple ones where the orders of reaction with respect to the various substances taking part are 0, 1 or 2. These tend to have the slow step of the reaction happening before any fast step(s).

To try to explain how fractional orders of reaction can arise is beyond the scope of UK A-level courses.

Here is the mechanism we have already looked at. How do we know that it works like this?

By doing rate of reaction experiments, you find this rate equation:

The reaction is first order with respect to the organic compound, and zero order with respect to the hydroxide ions. The concentration of the hydroxide ions isn't affecting the overall rate of the reaction.

If the hydroxide ions were taking part in the slow step of the reaction, increasing their concentration would speed the reaction up. Since their concentration doesn't seem to matter, they must be taking part in a later fast step.

Increasing the concentration of the hydroxide ions will speed up the fast step, but that won't have a noticeable effect on the overall rate of the reaction. That is governed by the speed of the slow step.

In a simple case like this, where the slow step of the reaction is the first step, the rate equation tells you what is taking part in that slow step. In this case, the reaction is first order with respect to the organic molecule – and that's all.

This gives you a starting point for working out a possible mechanism. Having come up with a mechanism, you would need to find more evidence to confirm it. For example, in this case you might try to detect the presence of the positive ion that is formed in the first step.

At first sight this reaction seems identical with the last one. A bromine atom is being replaced by an OH group in an organic compound.

However, the rate equation for this apparently similar reaction turns out to be quite different. That means that the mechanism must be different.

The reaction this time is first order with respect to both the organic compound and the hydroxide ions. Both of these must be taking part in the slow step of the reaction. The reaction must happen by a straightforward collision between them.

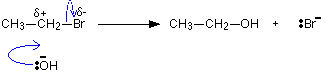
The carbon atom which is hit by the hydroxide ion has a slight positive charge on it and the bromine a slight negative one because of the difference in their electronegativities.

As the hydroxide ion approaches, the bromine is pushed off in one smooth action.

You may come across an older term known as the molecularity of a reaction. This has largely dropped out of UK A-level syllabuses, but if you meet it, it is important that you understand the difference between this and the order of a reaction. The terms were sometimes used carelessly as if they mean the same thing – they don't!

The important thing to realise is that this is something which can only be found by doing experiments. It gives you information about which concentrations affect the rate of the reaction. You cannot look at an equation for a reaction and deduce what the order of the reaction is going to be – you have to do some practical work!

Having found the order of the reaction experimentally, you may be able to make suggestions about the mechanism for the reaction – at least in simple cases.

This starts at the other end! If you know the mechanism for a reaction, you can write down equations for a series of steps which make it up. Each of those steps has a molecularity.

The molecularity of a step simply counts the number of species (molecules, ions, atoms or free radicals) taking part in that step. For example, going back to the mechanisms we've been looking at:

This step involves a single molecule breaking into ions. Because only one species is involved in the reaction, it has a molecularity of 1. It could be described as unimolecular.

The second step of this mechanism, involves two ions reacting together.

This step has a molecularity of 2 – a bimolecular reaction.

The other reaction we looked at happened in a single step:

Because of the two species involved (one molecule and one ion), this reaction is also bimolecular.

Unless an overall reaction happens in one step (like this last one), you can't assign it a molecularity. You have to know the mechanism, and then each individual step has its own molecularity.

There's nothing the least bit complicated about the term molecularity. The only confusion is that you may sometimes find it used as if it meant the same as order. It doesn't!

Relating orders of reaction to mechanisms is relatively easy where the slow step is the first step of the reaction mechanism. It isn't so easy when it is one of the later steps. I want to look at this in a bit more detail in case your syllabus requires it.

We will revisit the simple case first where the slow step is the first step of the mechanism.

Suppose you had a reaction between A and B, and it turned out (from doing some experiments) to be first order with respect to both A and B. So the rate equation is:

Which of these two mechanisms is consistent with this experimental finding?

Remember that in simple cases, where the slow step is the first step of the mechanism, the orders tell you what is taking part in the slow step.

In this case, the reaction is first order with respect to both A and B, so one molecule of each must be taking part in the slow step. That means that mechanism 2 is possible.

However, mechanism 1 must be wrong. One molecule of A is taking part in the slow step, but no B. The rate equation for that would be:

This is much more difficult to do and explain. I'm going to start with as simple example as possible

Suppose the mechanism for a reaction between A and B looks like this:

This time the slow step is the second step. Notice that the first (fast) step is reversible.

I need to assume that the fast step is much faster than the slow step – for reasons that I'm not going to explain. We are looking well beyond A level here!

The rate of the reaction will be governed by the slow step, and so the rate equation might look like this:

except, of course, that X isn't one of the things you are starting with!

At an introductory level, the flawed discussion often goes something like this:

As it happens, that gives the right answer in this case, but this simplistic view doesn't work in all cases – as I will show below.

So let's start again and do it better!

The rate of the reaction will be governed by the slow step, and so the rate equation might look like this:

except, of course, that X isn't one of the things you are starting with!

You need to be able to express the concentration of X in terms of [A] and [B], and you can do that because the first step is an equilibrium.

The equilibrium constant for the first reaction is:

You can rearrange this to give an expression for [X]:

and then substitute this value into the rate expression we started with:

If you sort this out, and combine the two different constants into a new rate constant, you get the rate expression:

So the reaction is second order with respect to A and first order with respect to B.

I am going to take another similar-looking example now, chosen to be deliberately awkward. This is to try to show that you can't reliably work these problems out just by looking at them.

This relates to the following reaction:

The mechanism for this is:

From the slow step of the reaction, the rate equation would like like this:

Up to now, this looks just the same as the previous example – but it isn't!

Let's do it properly, and think about the equilibrium expression for the first step in order to find a value for [X] that we can substitute into the rate equation.

The problem is that we have now got an extra variable in this equation that wasn't there before – we have got the concentration of Y. What do we do about that?

Well, for every mole of X formed, a mole of Y will be formed as well.

Provided that there was no X or Y in the mixture to start with, that means that the concentration of Y is equal to the concentration of X, and so we can substitute a value of [X] in place of the [Y], giving:

Rearranging that to get an expression for [X] gives:

And now you can substitute this into the rate equation:

and then tidy it up by combining the two constants into a single new rate constant:

The order is 0.5 with respect to both A and B, and 1 with respect to C.

There is no way you could have come up with that answer if you had just looked at the equations and assumed that the concentration of X is proportional to the concentrations of A and B.

The presence of the extra Y makes a serious difference to the result – but just looking at the equations, that isn't at all obvious.