Real Gases
This page looks at how and why real gases differ from ideal gases, and takes a brief look at the van der Waals equation. If you have come straight to this page via a search engine, it might be a good idea to read the page about ideal gases first.
Real Gases vs. Ideal Gases
Real Gases and the Molar Volume
I want to use this to illustrate the slight differences between the numerical properties of real and ideal gases at normal temperatures and pressures.
If you have read the page about ideal gases, you will remember that we used the ideal gas equation to work out a value for the molar volume of an ideal gas at stp (standard temperature and pressure).
If you know the density of a gas at a particular temperature and pressure, it is very easy to work out its molar volume.
For example, at 273 K and 1 atmosphere pressure, the density of helium is 0.1785 g dm-3.
That means that 0.1785 g of helium occupies 1 dm3 at stp. It is a fairly simple sum to work out what 1 mole of helium, He, would occupy.
1 mole of He weighs 4 g, and would occupy 4 / 0.1785 dm3 = 22.4 dm3.
That's the same (at least to 3 significant figures) as the ideal gas value, suggesting that helium behaves as an ideal gas under these conditions.
Note: If your maths isn't very good, and you can't understand why I divided 4 by 0.1785 to get the answer, think of it like this:
Replace the awkward value of 0.1785 by something simple, like 2. If 2 g of He occupied 1 dm3, what would 4 g occupy? It is obviously twice as much, 2 dm3 – but how did you get at that mathematically? You found out how many times 2 would go into 4 – in other words, you divided 4 by 2. Do exactly the same with the more complicated number.
If you do this for a random sample of other gases, you get these values (to 3 significant figures) for the molar volume at stp (273 K and 1 atmosphere pressure).
| density / g dm-3 | molar volume at stp / dm3 | |
|---|---|---|
| He | 0.1785 | 22.4 |
| N2 | 1.2506 | 22.4 |
| O2 | 1.4290 | 22.4 |
| CH4 | 0.717 | 22.3 |
| CO2 | 1.977 | 22.3 |
| C2H4 | 1.260 | 22.2 |
| NH3 | 0.769 | 22.1 |
| SO2 | 2.926 | 21.9 |
So although for simple calculation purposes we use the value 22.4 dm3 for all gases, you can see that it isn't exactly true. Even at ordinary temperatures and pressures, real gases can deviate slightly from the ideal value. The effect is much greater under more extreme conditions, as we will see next.
Compression Factors
For an ideal gas, pV = nRT. If pV and nRT are the same, and you divide one by the other, then the answer will, of course, be 1. For real gases, pV doesn't equal nRT, and so the value will be something different.
The term pV / nRT is called the compression factor. The graphs below show how this varies for nitrogen as you change the temperature and the pressure.
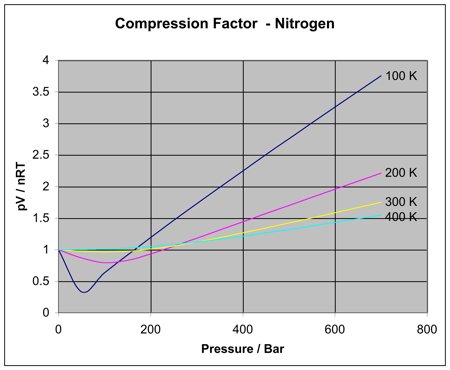
Note: These diagrams were generated using data produced from Patrick Barrie's program, and converted into graphs using Excel. The figures are derived from the van der Waals equation – not because it is the best source, but because it is the only one you are likely to come across at this level, and I shall mention it below. If you wanted to play around with some of the other equations, you would find that the results produce similarly shaped curves, but the absolute sizes of the deviations would vary.
If nitrogen was an ideal gas under all conditions of temperature and pressure, every one of these curves would be a horizontal straight line showing a compression factor of 1. That's obviously not true!
Things to notice
- At low pressures of about 1 bar (100 kPa – just a bit less than 1 atmosphere), the compression factor is close to 1. Nitrogen approximates to ideal behaviour at ordinary pressures.
- The non-ideal behaviour gets worse at lower temperatures. For temperatures of 300 or 400 K, the compression factor is close to 1 over quite a large pressure range. The nitrogen becomes more ideal over a greater pressure range as the temperature rises.
- The non-ideal behaviour gets worse at higher pressures.
- There must be at least two different effects causing these deviations. There must be at least one effect causing the pV / nRT ratio to be too low, especially at low temperatures. And there must be at least one effect causing it to get too high as pressure increases. We will explore those effects in a while.
Other gases
Is the same behaviour shown by other gases? The next diagram shows how the compression factors vary with pressure for a variety of gases at a fixed temperature.
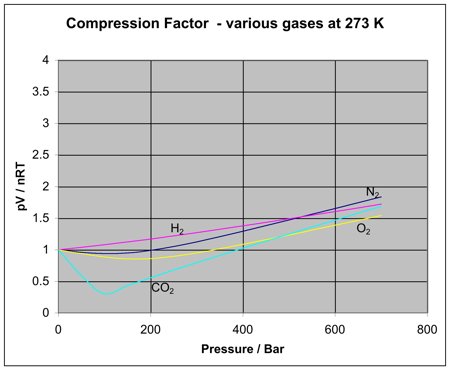
If you were to redo the set of original nitrogen graphs (at varying temperatures) for any of these other gases, you would find that each of them will produce a set of curves similar to the nitrogen ones. What varies is the temperature at which the different graph shapes occur.
For example, if you look at the carbon dioxide graph at 273 K, it looks similar to the nitrogen one at 100 K from the first set of curves, although it doesn't increase so steeply at higher pressures.
It is easy to say that gases become less ideal at low temperatures, but what counts as a low temperature varies from gas to gas. The closer you get to to the temperature at which the gas would turn into a liquid (or, in the case of carbon dioxide, a solid), the more non-ideal the gas becomes.
What Causes Non-ideal Behaviour?
In the compression factor expression, pV / nRT, everything on the bottom of the expression is either known or can be measured accurately. But that's not true of pressure and volume.
In the assumptions we make about ideal gases, there are two statements which say things which can't be true of a real gas, and these have an effect on both pressure and volume.
The volume problem
The kinetic theory assumes that, for an ideal gas, the volume taken up by the molecules themselves is entirely negligible compared with the volume of the container.
For a real gas, that assumption isn't true. The molecules themselves do take up a proportion of the space in the container. The space in the container available for things to move around in is less than the measured volume of the container.
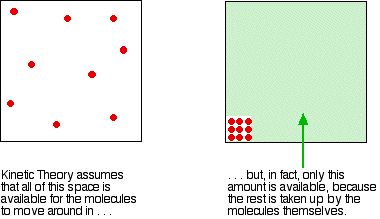
This problem gets worse the more the gas is compressed. If the pressure is low, the volume taken up by the actual molecules is insignificant compared with the total volume of the container.
But as the gas gets more compressed, the proportion of the total volume that the molecules themselves take up gets higher and higher. You could imagine compressing it so much that the molecules were actually all touching each other. At that point the volume available for them to move around in is zero!
Suppose at some high pressure, you measure the volume of the container as, say, 1000 cm3, but suppose the molecules themselves occupy as much as 100 cm3 of it.
The ideal gas equation was worked out by doing calculations based on Kinetic Theory assumptions. The V in pV is assumed to be the volume which the molecules are free to move around in – but in this case, it would only be 900 cm3, not 1000 cm3.
If you worked out the compression factor, pV / nRT, by putting the total volume of the container into the formula, the answer is bound to be higher than it ought to be. It doesn't allow for the volume taken up by the molecules themselves.
Let's just repeat one of the earlier diagrams so that you can see this effect in operation.

For an ideal gas, the compression factor would be 1 over the whole pressure range. For a real gas like nitrogen, notice how the compression factor tends to increase with pressure.
The value of the compression factor is too high at high pressures for a real gas. The reason for that is that the measured volume that you put into the expression is too high because you aren't allowing for the volume taken up by the molecules. That error gets relatively worse the more compressed the gas becomes.
The pressure problem
Another key assumption of the Kinetic Theory for ideal gases is that there are no intermolecular forces between the molecules. That is wrong for every real gas.
If there weren't any intermolecular forces then it would be impossible to condense the gas as a liquid. Even helium, with the weakest of all intermolecular forces, can be turned to a liquid if the temperature is low enough.
So what effect do intermolecular forces have?
For a gas molecule in the middle of the gas, there is no net effect. It will be attracted to some extent to all the other molecules around it, but, on average, those attractions will cancel each other out. Attractions from behind a molecule, tending to slow it down, will be cancelled out by attractions from in front of it, tending to speed it up.
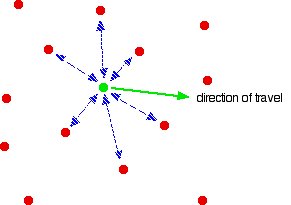
Despite all the intermolecular forces it is experiencing, the molecule picked out in green will just continue to move in the same direction at the same speed.
That's different if the molecule is just about to hit the wall of the container.
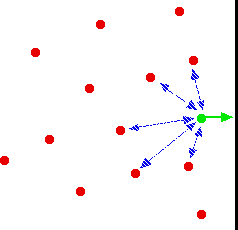
Now there aren't any gas molecules in front of it, and the net pull is backwards into the body of the gas. The molecule will slow down just before it hits the wall.
If it slows down, it will hit the wall less hard, and so exert less pressure.
The overall effect of this is to make the measured pressure less than it would be if the gas was ideal. That means that if you put the measured pressure into the expression pV / nRT, the value of the compression factor will be less than it would be if the gas was ideal.
This is why, under some conditions, graphs of compression factors drop below the ideal value of 1.
Look yet again at the nitrogen curves:

This effect is most important at low temperatures. Why is that?
At lower temperatures, the molecules are moving more slowly on average. Any pull they feel back into the gas will have relatively more effect on a slow moving particle than a faster one.
At higher temperatures, where the molecules are moving a lot faster, any small pull back into the body of the gas is hardly going to be noticeable. At high temperatures, the effect of intermolecular forces is indeed negligible.
And there is one final effect concerning intermolecular forces which is slightly more hidden away.
As pressure increases, the molecules are forced more closely together. If they are closer, the intermolecular forces will become more important. So, as pressure increases, you would expect more lowering of the compression factor relative to the ideal case. The molecules which slow down the one just about to hit the wall will be closer to it, and so more effective.
Is that what happens? Yes, up to a point.
Look again at the nitrogen curve at 100 K. As the pressure increases, at first the value of the compression factor falls.
But it soon starts to rise again. Why? Because at this point, the effect of the size of the molecules starts to become more important – and as the pressure is increased even more, this other effect becomes dominant.
Which is the Most Ideal Gas?
You are looking for a gas with the smallest possible molecules, and the lowest possible intermolecular forces. That is helium.
A helium molecule consists of a single small atom, and the van der Waals dispersion forces are as low as it is possible for them to be.
Note: If you aren't happy about the factors which affect the size of van der Waals dispersion forces, follow this link.
Like helium, a hydrogen molecule also has two electrons, and so the intermolecular forces are going to be small – but not as small as helium. In the hydrogen molecule, you have two atoms that you can distribute the charges over.
As molecules get larger, then dispersion forces will increase, and you may get other intermolecular forces such as dipole-dipole attractions as well. Gases made of molecules such as these will be much less ideal.
The van der Waals Equation
The van der Waals equation was the first attempt to try to produce an equation which related p, V, n and T for real gases. It looks like this:
If you think this looks complicated, you should see some of the more modern attempts! Incidentally, you may come across the equation in a simpler form for 1 mole of a gas rather than for n moles. Under those circumstances, every single n in the equation disappears.
Look at the left-hand side in two stages. First the pressure term.
Remember from above, that the measured pressure is less than the ideal pressure for a real gas. van der Waals has added a term to compensate for that.
In the volume term, van der Waals has subtracted the value nb to allow for the space taken up by the molecules themselves.
a and b are constants for any particular gas, but they vary from gas to gas to allow for the different intermolecular forces, and molecular sizes. That means that, unfortunately, you no longer have a single equation that you can use for any gas.
Fortunately, however, the ideal gas equation works well enough for most gases at ordinary pressures, as long as the temperature is reasonably high.
Where would you like to go now?
To the kinetic theory menu To the Physical Chemistry menu To Main Menu