The Effect of Pressure on Rates of Reaction

This page describes and explains the way that changing the pressure of a gas changes the rate of a reaction.

The Facts

What Happens?

Increasing the pressure on a reaction involving reacting gases increases the rate of reaction. Changing the pressure on a reaction which involves only solids or liquids has no effect on the rate.

An Example

In the manufacture of ammonia by the Haber Process, the rate of reaction between the hydrogen and the nitrogen is increased by the use of very high pressures.

\text{N}_{2(g)} + 3\text{H}_{2(g)} \xrightleftharpoons{} 2\text{NH}_{3(g)}

In fact, the main reason for using high pressures is to improve the percentage of ammonia in the equilibrium mixture, but there is a useful effect on rate of reaction as well.

Note: If you want to explore equilibria you will find the topic covered in a separate section of the site.

The Explanation

The Relationship Between Pressure and Concentration

Increasing the pressure of a gas is exactly the same as increasing its concentration. If you have a given mass of gas, the way you increase its pressure is to squeeze it into a smaller volume. If you have the same mass in a smaller volume, then its concentration is higher.

You can also show this relationship mathematically if you have come across the ideal gas equation:

\begin{gathered} pV = nRT \\ \\ \begin{aligned} p~-&~\text{pressure} \\ V~-&~\text{volume} \\ n~-&~\text{number of moles} \\ R~-&~\text{gas constant} \\ T~-&~\text{temperature in Kelvin} \end{aligned} \end{gathered}

Rearranging this gives:

\begin{gathered} p = \frac{n}{V} \times \overbrace{RT}^{\clap{\text{\color{#467abf}{constant at constant temperature}}}{}} \\ \\ \begin{aligned} p~-&~\text{pressure} \\ \frac{n}{V}~-&~\text{number of moles divided by volume = concentration} \end{aligned} \end{gathered}

Because "RT" is constant as long as the temperature is constant, this shows that the pressure is directly proportional to the concentration. If you double one, you will also double the other.

Note: If you should be able to do calculations involving the ideal gas equation, but aren't very happy about them, you might be interested in my chemistry calculations book.

The Effect of Increasing the Pressure on the Rate of Reaction

Collisions involving two particles

The same argument applies whether the reaction involves collision between two different particles or two of the same particle.

In order for any reaction to happen, those particles must first collide. This is true whether both particles are in the gas state, or whether one is a gas and the other a solid. If the pressure is higher, the chances of collision are greater.

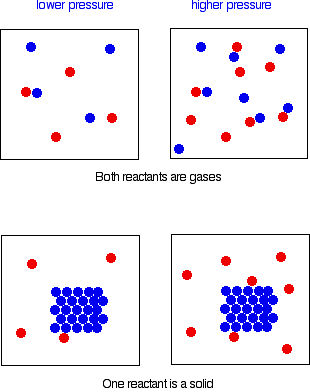
Reactions involving only one particle

Things get more difficult to explain if you have reactions involving something happening to a single particle rather than being caused by a collision between two particles. The relationship between pressure and rate is much more complicated and varies from reaction to reaction. This is beyond A level.

Note: There are theories which show that even for unimolecular reactions (reactions only involving one molecule) collisions are necessary in order for molecules to gain activation energy. If you want to know more about this, you will have to do chemistry to a higher level. You could google it, but you will find explanations are at a high level and quite mathematical.

Where would you like to go now?

To the rates of reaction menu To the Physical Chemistry menu To Main Menu